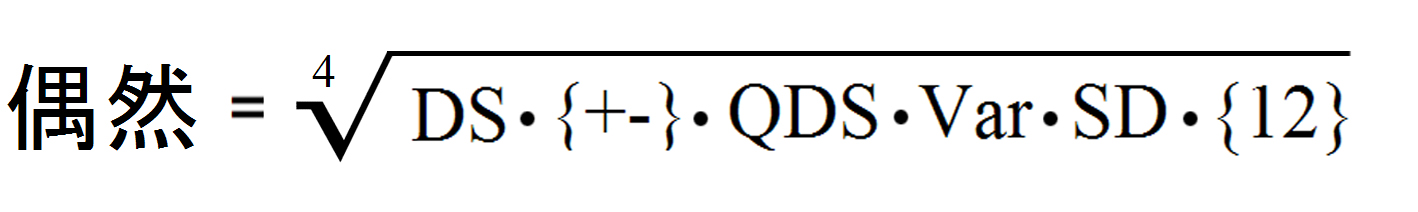1,414213562373095048801688724209698078569671
87537694807317667973799073247846210703885038
75343276415727350138462309122970249248360558
50737212644121497099935831413 ...
Die Zahl wird Ihnen vermutlich bekannt vorkommen. Sie sieht so aus wie die Wurzel aus 2. Zumindest sind ihre Stellen bis zu der Stelle, wo sie abbricht, mit denen der Wurzel aus 2 identisch.
Vorstellbar wäre, dass die Zahlenfolge sich ab dieser Stelle zu wiederholen beginnt, wie es mit ganzen Zahlen darstellbare Brüche tun. Wie wäre es mit 100.000 / 70711? Die ersten fünf Stellen nach dem Komma - 1,41421 - haben beide Zahlen tatsächlich gemeinsam.
Sie bräuchten folglich, um die Wurzel aus 2 mit einem Bruch aus ganzen Zahlen darstellen zu können, zwei unendlich lange Zahlen, was die mathematischen Definitionen verletzt ... weshalb man Zahlen wie diese in der Gruppe der irrationalen Zahlen zusammenfasst.
Unter diesen Irrationalzahlen gibt zwei Typen:
Die Algebraische Zahlen (etwa Wurzeln, z.B. , )
und
Die Transzendenten Zahlen (z. B. die Kreiszahl p = 3,14159... oder die Eulersche Zahl e = 2,71828...).
Irrationalzahlen durchlaufen im Gegensatz zu periodischen Zahlen das Zahlenspektrum scheinbar willkürlich, man könnte eine zufällige Reihung vermuten - bzw. eine pseudozufällige Reihung, denn welche Zahl auf die nächste ist, mathematisch besehen, kein Zufall, sondern eine Notwendigkeit.
Die Schwierigkeit aber, aus den vorherigen Zahlen nur durchs bloße Ansehen die nächste Zahl zu erraten, lässt eine solche Zahl schnell merkwürdig oder mysteriös erscheinen. Wiewohl sich, beim näheren Hinsehen, auch deutliche Gesetzmäßigkeiten innerhalb ihrer Anordnung finden lassen.
Nehmen wir nur einmal die profane Zahlenhäufigkeit. Betrachten wir die ersten 10.000 Stellen der Goldenen Zahl Phi. Wie häufig sind nun die jeweiligen Zahlen bei Phi verteilt?
Ziehen wir zum Vergleich eine Wurzel heran, die 2. Wurzel aus 10 . Sie zeigt noch geringere Abweichungen von dem Erwartungswert 1.000 bei 10.000 Nachkommastellen:
Wählen wir eine nicht-irrationale Zahl: Eine Zahl, die sich als Bruch darstellen lässt wie zum Beispiel 1 / 1234567 . Bei den ersten 10.000 Stellen lässt sich noch keine Periodizität nachweisen, es ist aber anzunehmen, dass sie eine periodische Struktur besitzt. Es ist erstaunlich: Auch sie zeigt noch sehr geringe Abweichungen von dem Erwartungswert 1.000, ist kaum von den irrationalen Zahlen zu unterscheiden:
Wählen wir unter den nicht-irrationalen Zahlen einen einfacheren Bruch:
1 / 1234 . Hier ist die Periodizität offensichtlich, die Zahlenfolge ...00810372771474878444084278768233387358184764
99189627228525121555915721231766612641815235...
mit insgesamt 88 Zahlen wiederholt sich 113mal bei den ersten 10.000 Stellen. Da innerhalb dieser Periode die Zahlen ungleich häufig verteilt sind, wird hier der Erwartungswert von 1.000 oft deutlich über- oder unterschritten. Hier würde gewiss niemand mehr von Zufälligkeit sprechen wollen:
Wie man sieht, weist dieser Bruch zudem eine Symmetrie auf. Die Zahlen 4 und 5 sind gleichhäufig, ebenso 3 und 6, 2 und 7, 1 und 8 sowie 0 und 9.
Wie man sieht, verhelfen die Diagramme mit den Zahlenhäufigkeiten nur zu einer oberflächlichen Einschätzung der - ich nenne es hier einmal Zufallsstruktur einer Zahlenfolge. Man kann aus den Abweichungen beispielsweise die Varianz und die Standardabweichung ermitteln. In unserem Fall käme man auf folgendes Abweichungs-Ranking bei den vier Zahlenfolgen (zuzüglich der Kreiszahl Pi als weiterer Vergleich):
Varianz / Standardabweichung
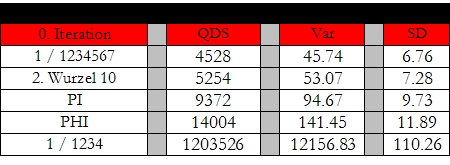
Die Begriffe QDS, VAR und SD werde ich im weiteren Verlauf noch en detail erklären. Um es abzukürzen: Varianz und Standardabweichung definieren die durchschnittliche Abweichung der Erwartungswerte, also die Schwankungen um den Durchschnittswert.
Dieses Ergebnis ist verblüffend: Der Bruch 1/1234567 ist von geringerer Schwankung als Phi oder Pi, jene irrationalen Zahlen, die für ihre Irrationalität berühmt sind. Und selbst die Wurzel aus 10 hat geringere Ausreißer.
Was heißt das? Nur einmal angenommen, dieses Ergebnis bezöge sich nicht nur auf die ersten 10.000 Stellen, sondern 10.000x10.000 Stellen ... was würde das dann bedeuten? Dass 1/1234567 eine besonders zufällige Zahl ist?
Nicht unbedingt! Denn es wäre auch ein Ergebnis mit einer Varianz von 0 denkbar! Eine, die 10x für jeden der zehn Zahlenwerte exakt 1.000x eine dieser Zahlen verwendet.
Denken Sie nur an die Zahlenfolge 012345678998765432100123456789987...
Wenn Sie diese Folge ins Unendliche fortschreiben, erhalten sie genau ein solches Ergebnis: Varianz und Standardabweichung 0!
Woraus man folgern könnte: Eine Zahl, die eine sehr geringe bis gar nicht vorhandene Varianz/Standardabweichung aufweist, ist weniger zufällig als eine Zahl wie die Goldene Zahl Phi oder Pi, die eine gewisse Streuung aufweisen, wenngleich die Streuung nicht zu deutlich und markant ausfällt wie etwa beim Bruch 1/1234.
Dieses Ergebnis verblüfft: Womöglich, könnte man nun mutmaßen, liegt die wahrhaft irrationalste aller Zahlen irgendwo zwischen den sehr geringen und sehr hohen Varianz- und Standardabweichungswerten.
Eine geringe Varianz lässt somit ein Schema vermuten, nach dem die nächsten Werte sich an die vorangegangenen anfügen, es gibt in einem solchen Fall also vermutlich ein System und kein pures Nichtsystem. Ebenso haben Reihen mit hoher Varianz meistens ein Schema - das Schema einer zu großen Ordnung bzw. von Präferenzen für bestimmte Zahlen.
Während also eine sehr geringe und eine hohe Varianz auf eine Ordnung schließen lassen, müssten die Mittelwerte die zufälligsten Zahlenfolgen aufweisen. Wenn also Pi und Phi in der Mitte dieser Skala hier stehen, könnte man das damit erklären, dass hier die chaotische Struktur von Zahlen von beiden Seiten durch geordnete Systeme umarmt, eingefasst wird.
Selbstverständlich ist das noch kein überzeugendes Kriterium. Wir nähern uns damit erst dem Phänomen von Ordungsstrukturen und Chaosstrukturen bei den Zahlenfolgen an.
Ich habe in einer ersten Analyse 20 zufällig aussehende Zahlenfolgen (die meisten davon, sofern ich das beurteilen konnte, sind Irrationalzahlen) mit ihren ersten 1.000 Nachkommastellen nach dem obigen Schema der Varianz und der Standardabweichung untersucht. Ich habe aber auch noch weitere informative Aspekte mit in die Berechnung einbezogen. Woraus ich eine Formel entwickelt habe, die den Grad der Abweichung definiert:
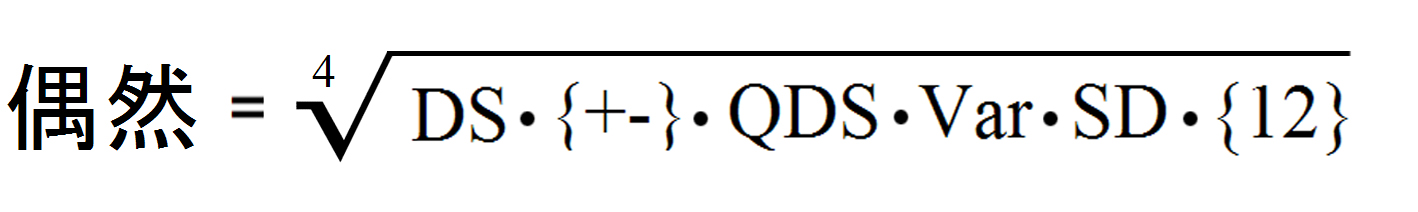
Was sich wie folgt aufschlüsselt:
| DS
|
Differenz-Summe (Abweichungen vom Mittelwert, summiert)
|
| {+-}
|
Abweichungen Zahlenwert 0/1 + 1/2 + 2/3 ... + 8/9 + 9/0
|
| QDS
|
Quadrate der Differenzen, summiert
|
| Var
|
Die Varianz. QDS/(n-1)
|
| SD
|
Die Standardabweichung. SD = Wurzel (var)
|
| {12}
|
Größere Summe/Kleinere Summe. {1} setzt sich zusammen aus den Zahlwerten 0-4, {2} aus den Zahlwerten 5-9
|
ist das chinesische Schriftzeichen für Zufall bzw. "zufällig"). hat sechs Komponenten oder Kriterien, von denen jedes einzelne den Grad von Zufälligkeit bereits in Maßen beschreibt.
Die Differenzsumme (DS) ähnelt hierbei der Quadratdifferenzsumme (QDS), und mit der Varianz (Var) erzeugt man sogar eine identische Reihenfolge wie mit der Standardabweichung (SD), wenn man eine Art Zufalls-Ranking aufstellen möchte. Die beiden eckig umklammerten Werte {+-} und {12} beschreiben die Nachbarschaften von den einzelnen Zahlwerten.
Bei {+-} wird eine Folge wie etwa diese Häufigkeitsverteilung der Goldenen Zahl Phi (siehe oben):
0=1019
1=1062
2=994
3=1038
4=976
5=988
6=918
7=1025
8=987
9=991
bewertet nach dem Verlauf der Kurve (wie bei dem obigen Diagramm, welches lesbar wäre von links nach rechts oder umgekehrt). Erst vergleicht man die Werte 0 und 1, in diesem Fall ergibt 1062-1019 den Zahlwert "43". Dann vergleicht man 1 und 2 und bildet die Differenz. Aus den 10 Differenzen, die man erhält, ermittelt man die Beträge und summiert sie - und erhält dann den Wert {+-}, der in die Berechnung von eingeht.
Mit {12} ermittelt man, ob es ein ausgewogenes Gleichgewicht aus den niedrigen Zahlbereich von 0-4 und dem hohen Zahlbereich von 5-9 gibt. (An diese Stelle wäre zu überlegen, ob man auch noch ein Wert für den Faktor Gerade-Ungerade ermittelt, also ein {GU}.)
Damit der Wert von nicht vielstellig wird, ermittelt man aus dem Produkt der sechs Formelkomponenten die vierte Wurzel. Es könnte auch die sechste oder achte Wurzel sein - der Wert an sich spielt keine Rolle. Allein schon deshalb, weil er deutlich variiert, wenn man beispielsweise 10.000 Nachkommastellen betrachtet oder 1.000.000. ist somit nur dann als Zahlwert vergleichbar, wenn man die gleiche Zahlenmenge berücksichtigt hat.
Sie werden interessiert sein, was bei dem ersten Zufalls-Ranking herauskam. Sie können es hier unter einsehen.
: