Der Parameter {12} analysiert die Neigung einer Zahlenfolge zu einer Seite des Zahlenspektrums. Man muss hierbei die zehn Zahlen eines 10er-Zahlensystems nicht automatisch in {1}= [0,1,2,3,4] und {2}= [5,6,7,8,9] einteilen, es wären auch andere Einteilungen denkbar. Dass die fünf Zahlen zusammenhängen, ist allerdings durchaus gewünscht (wenn auch nicht unbedingt notwendig), also etwa {1}= [3,4,5,6,7] und {2}= [8,9,0,1,2].
Der Parameter {12} bestimmt dann die Tendenz einer Zahlenfolge, sich zu einer Seite zu neigen oder zur anderen, mit ihm kann man analysieren, ob die Neigungen in Schwingungen verlaufen, die an Sinus-Schwingungen erinnern usw..
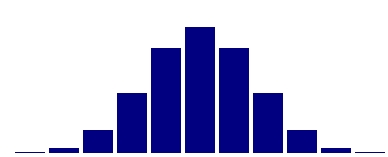
Die 0. Iteration der Goldenen Zahl Phi sieht als {12} mit
{1}= [0,1,2,3,4] und
{2}= [5,6,7,8,9]
unter Verwendung der ersten 5.000 Stellen (zerschnitten in hundert 10er-Zahlenfolgen) wie folgt aus:
Eine hübsche Glockenkurve, wird man nun erklären - unwidersprochen! Und etwas anderes hätte man auch nicht erwarten können, nicht wahr?
Nur zeigt diese Verteilung tatsächlich einen idealen Zufall an? Man kann sie gegenlesen beispielsweise mit den ersten 5.000 Nachkommastellen der Kreiszahl Pi - und deren Ergebnis verblüfft:
Offensichtlich weicht Pi nicht nur zu beiden Seiten ab von der klassisch-statistischen Glockenkurve und sieht eigenartig windschief aus, Pi zeigt im Vergleich zu Phi überdies einen deutlich höheren Anteil an Werten genau in der Mitte im Verhältnis 5:5, oder anders notiert:
Häufigkeit ( H{0} = H{1} )
Phi weist 115 gleichverteilte Häufigkeiten (von insgesamt 500 10er-Zahlenfolgen) auf, was 23,00 Prozent entspricht. Pi hingegen kommt auf 27,00 Prozent.
Überlegung:
Vorausgesetzt, dieser Unterschied bestätigt sich an allen weiteren 5.000 Stellen der jeweiligen Zahlen - dann kann man folglich diesen irrationalen Zahlen einen besonderen {12}-Charakter diagnostizieren. Was folgende Schlussfolgerung ergäbe: Es könnte aufgrund ihrer Verschiedenheit nur entweder Pi oder Phi den idealen Zufall aufweisen - noch wahrscheinlicher aber ist, dass weder Pi noch Phi ideal zufällig sind.
Aufgrund des Kurvenverlaufs scheint Phi durch seine Symmetrie eher dem zu erwartenden Zufall zu entsprechen, die fehlende Symmetrie bei Pi wiese demnach auf eine Struktur hin. Sollte sich Pi´s {12}-Struktur nun tatsächlich über die gesamte Zahlenfolge erstrecken, was wäre daraus zu folgern? Es hieße, dass Pi eine Struktur besitzt, und dass man unter Anwendung des Wissens über diese Struktur die folgende Nachkomma-Stellenzahl mit einer größeren Wahrscheinlichkeit als 10 Prozent angeben kann.
Als ersten Vergleich möchte ich einen Mechanismus heranziehen, der versucht, Zufall zu simulieren: Den Roulette-Kessel. Die Permanenzen wurden von einem Tisch des Casino Wiesbaden am 01.01.2008 entnommen, wobei nur die Zahlen 0-29 in die Statistik eingingen in Gestalt der Endziffer - um eine 10er-Zahlenfolge zu generieren. Aus der gewonnenen Zahlenfolge konnte ich 47 10er-Zahlenfolgen in den {12}-Parameter übertragen:
Eine Glockenkurve kann man bei 47 Ereignissen nur in Ansätzen erwarten. An dieser Kure auffällig ist vor allen Dingen aber die hohe Anzahl der gleichverteilten Häufigkeiten, in 19 von 47 Fällen war das Verhältnis 5:5, was einen Prozentanteil von 40,42 Prozent, womit diese Zahlenfolge weit über denen von Pi und Phi liegt.
Was nun sind aber die zu erwartenden Wahrscheinlichkeiten im Falle eines idealen Zufalls? Es sind bei 10 Ereignissen und zwei Möglichkeiten insgesamt 1024 Verläufe denkbar, die zu folgender idealen Wahrscheinlichkeitsverteilung führen - selbstverständlich ist es eine Glockenkurve: